This January 2009 help sheet gives information on how to obtain:

• Probabilities and inverse probabilities in Excel
• T-Distribution probabilities and inverse probabilities
• Normal distribution probabilities and inverse probabilities
• Othrr distributions
  
• Random draws from distributions such as the normal.

PROBABILITIES AND INVERSE PROBABILITIES

We consider the standard normal distribution as an example.

Let X be random variable, x be a value of the random variable, and p be a probability. Then:

• A probability such as Pr(X <= x) is given by the cumulative distribution function.
  So the Excel command includes "DIST"
  e.g. TDIST for the T distribution
  e.g. NORMSDIST for the standard normal distribution
  e.g. NORMDIST for the normal distribution

• A value of x such that Pr(X <= x) = p for some specified value of  p is called the inverse of the cumulative distribution function.
  So the Excel command includes "INV"
  e.g. TINV for the T distribution
  e.g. NORMSINV for the standard normal distribution
  e.g. NORMINV for the normal distributio
  


• These functions are given in Formulas Tab | Function Library Group | More Functions | Statistical.

T-DISTRIBUTION PROBABILITIES AND INVERSE-PROBABILITIES

These are the most commonly-used probabilities in statistical analysis of economics data.
These use the TDIST and TINV functions.

TDIST gives the probability of being in the right tail i.e. Pr(X > x), or of being in both tails i.e. Pr(|X| > x).
TINV considers the inverse of the probability of being in both tails.

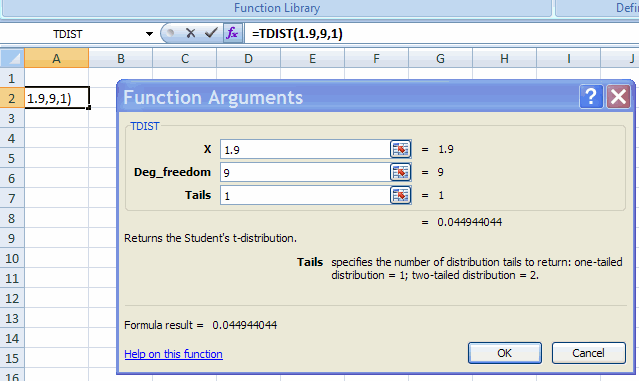
1. Find Pr(X <= 1.9) when x is t-distributed with 9 degrees of freedom.

This is 1 - Pr(X > 1.9) where Excel function TDIST gives Pr(X > 1.9).

Choose Formulas Tab | Function Library Group | More Functions | Statistical | TDIST.
Fill in the Function Arguments Tab:

This gives result that Pr(X > 1.9) = 0.0449.
So Pr(X <= 1.9) = 1 - 0.0449 = 0.9551.

Much simpler is to directly type in the cell = 1 - TDIST(1.9, 9, 2) and hit <enter>.

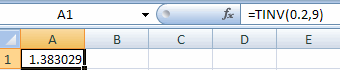
2. Find the value x* such that Pr(X <= x*) = 0.9 when x is t-distributed with 9 degrees of freedom.

This is the same value as that for which Pr(|X| >= x*) = 0.2.
(Since there is probability 0.1 in the right tail and  probability 0.1 in the left tail).

Choose Formulas Tab | Function Library Group | More Functions | Statistical | TINV.
Fill in the Function Arguments Tab:

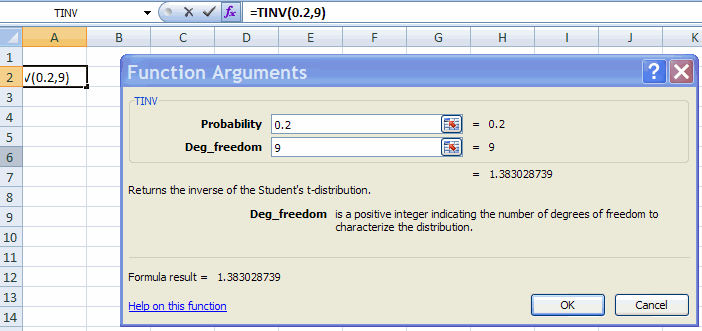
This gives result that Pr(|X| > 1.383) = 0.2.
So Pr(X <= 1.383) = 0.9.

STANDARD NORMAL PROBABILITIES AND INVERSE-PROBABILITIES

These are less used than the t-distribution in statistical analysis of economics data.
These use the NORMDIST and NORMINV functions.

IMPORTANT: The format and results of these commands differ from those for the normal.
NORMDIST directly gives the cumulative distribution function i.e. Pr(X <= x), whereas TDIST instead gives the right tail, i.e. Pr(X > x) !!
NORMINV considers the inverse of the probability of being in both tails, similar to TINV.

1. Find Pr(X <= 1.9) when x is standard normal (i.e. normal with mean=0 and variance=1).

Choose Formulas Tab | Function Library Group | More Functions | Statistical | NORMDIST.
Fill in the Function Arguments Tab with Z value of 1.9.
This gives result that Pr(X <= 1.9) = 0.9713.

Much simpler is to directly type in the cell  =NORMSDIST(1.9) and hit <enter> to get Pr(X <= 1.9) = 0.9713.

2. Find the value x* such that Pr(X <= x*) = 0.9 when x is standard normal.

Choose Formulas Tab | Function Library Group | More Functions | Statistical | NORMDIST.
Fill in the Function Arguments Tab with probability value of 0.9.
This gives result that x* = 1.2816,  i.e. Pr(X <= 1.2816) = 0.9.

Much simpler is to directly type in the cell  = NORMSINV(0.9) and hit <enter> to get  x* = 1.2816.
 

The standard normal sets the mean to 0 and standard deviation to 1.
Here we consider the normal distribution with other values for the mean µ and standard devation σ.
THE functions used are NORMDIST and NORMINV.

1. Find Pr(X <= 9) when x is normal with mean µ =8 and variance 4.8.
Here standard deviation = σ = sqrt(4.8) = 2.1909.

Choose Formulas Tab | Function Library Group | More Functions | Statistical | NORMDIST.
Fill in the Function Arguments Tab

 

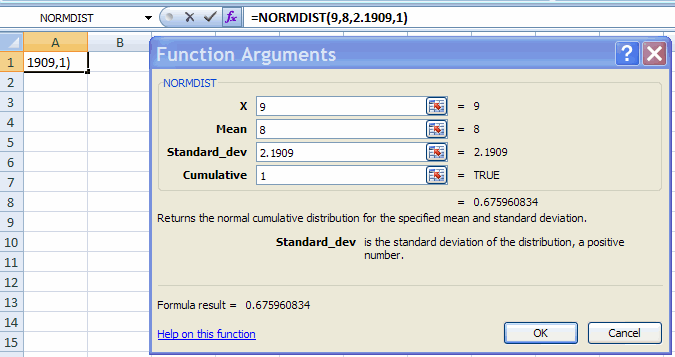
This gives result that Pr(X > 9) = 0.67596 for X normally distributed wuith mean 8 and variance 4.8.

Much simpler is to directly type in the cell  = NORMDIST(9, 8, 2.1909, 1) and hit <enter>.

2. Find the value x* such that Pr(X <= x*) = 0.9 when x is normal with mean µ =8 and variance 4.8, so standard deviation = σ = sqrt(4.8) = 2.1909.

Choose Formulas Tab | Function Library Group | More Functions | Statistical | NORMINV.
Fill in the Function Arguments Tab:

 

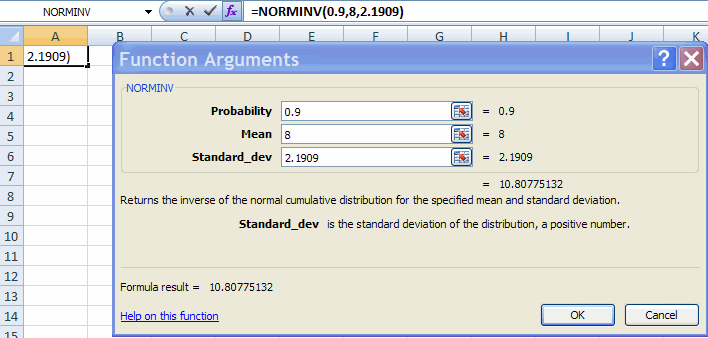
probability	0.9
mean	8
standard_dev	2.1909

This gives result x* =  10.8077.  i.e. Pr(X < 10.8077) = 0.9  when x is normal with mean µ =8 and variance 4.8.

Much simpler is to directly type in the cell  = NORMINV(0.9, 8, 2.1909) and hit <enter>.

OTHER DISTRIBUTIONS

Excel provides probabilities for the following distributions (in Formulas Tab | Function Library Group | More Functions | Statistical), presented in approximate order of most commonly used in the analysis of economics data:

• Normal: NORMDIST, NORMINV
• Standard normal: NORMSDIST, NORMSINV
• t-distribution: TDIST, TINV
• F-distribution: FDIST, FINV
• Chi-square: CHIDIST, CHIINV
• Lognormal: LOGNORMDIST, LOGINV
  
• Binomial: BINOMDIST, CRITBINOM
  
• Hypergeometric: HYPGEOMDIST
• Beta: BETADIST, BETAINV
• Gamma: GAMMADIST, GAMMAINV
• Exponential: EXPONDIST
• Weibull: WEIBULL
• Poisson: POISSON
• Negative binomial: NEGBINOMDIST

RANDOM NUMBER GENERATION

It can be useful to generates a random sample of observations from a specified distribution, such as the standard normal.

Use Data Tab | Analysis Group | Data Analysis.
This permits generation from

• Normal
• Uniform
• Bernoulli (0 or 1)
• Binomial
• Poisson
• Discrete (you provide the values and probabilities for a discrete distribution with finite number of possible values)
• Patterned

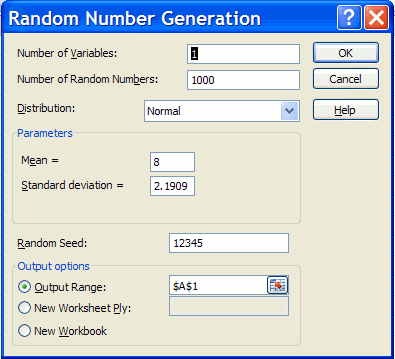
Generate 1000 values of x where x is normal with mean mu = 8 and variance 4.8, so standard deviation = sigma = sqrt(4.8) = 2.1909.

Choose Data | Analysis | Data Analysis | Random Number Generation.
Then in the Random Number Generation dialog box fill in:

 

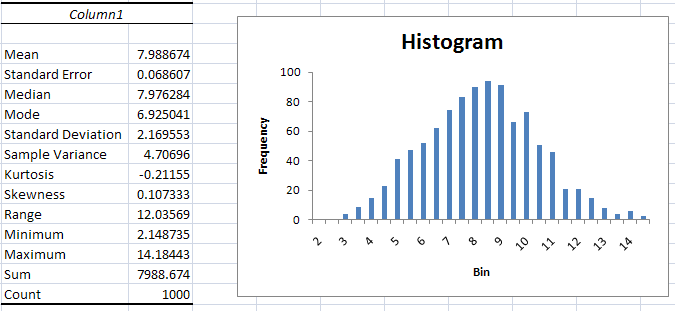
The 1,000 random draws have sample mean close to 8, sample variance close to 4.8, and histogram that is close to a bell-shaped curve.

For further information on how to use Excel see
   http://cameron.econ.ucdavis.edu/excel/excel.html