• Interpreting the regression statistics.
• Interpreting the ANOVA table (often this is skipped).
• Interpreting the regression coefficients table.
• Confidence interval for the slope parameter.
  
• Testing hypothesis of zero slope parameter.
• Testing hypothesis of slope parameter equal to a particular value other than zero.
• Testing overall significance of the regressors.
• Predicting y given values of regressors.
• Fitted values and residuals from regression line.
• Other regression output.
  

REGRESSION USING THE DATA ANALYSIS ADD-IN

This requires the Data Analysis Add-in: see Excel 2007: Access and Activating the Data Analysis Add-in
The data used are in carsdata.xls
The method is explained in Excel 2007: Two-Variable Regression using Data Analysis Add-in

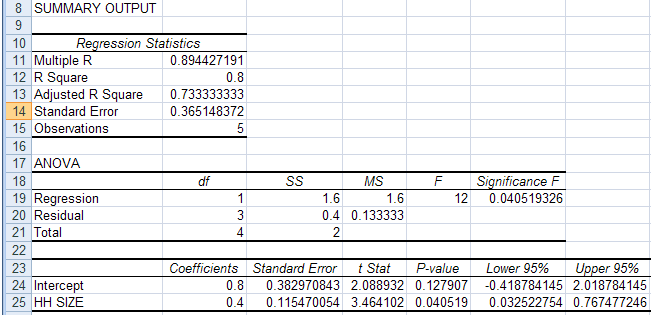
Regression of CARS on HH SIZE led to the following Excel output:

The regression output has three components:

• Regression statistics table
• ANOVA table
• Regression coefficients table.

INTERPRET REGRESSION STATISTICS TABLE
 

		Explanation
Multiple R	0.894427	R = square root of R2
R Square	0.8	R2 = coefficient of determination
Adjusted R Square	0.733333	Adjusted R2 used if more than one x variable
Standard Error	0.365148	This is the sample estimate of the standard deviation of the error u
Observations	5	Number of observations used in the regression (n)

The Regression Statistics Table gives the overall goodness-of-fit measures:
      R² = 0.8
      Correlation between y and x is 0.8944 (when squared gives correlation squared = 0.8 = R² ).
      Adjusted R²  is discussed later under multiple regression.

The standard error here refers to the estimated standard deviation of the error term u.
It is sometimes called the standard error of the regression. It equals sqrt(SSE/(n-k)).
It is not to be confused with the standard error of y itself (from descriptive statistics) or with the standard errors of the regression coefficients given below.
 

INTERPRET ANOVA TABLE
 

	df	SS	MS	F	Signifiance F
Regression	1	1.6	1.6	12	0.04519
Residual	3	0.4	0.133333
Total	4	2.0

The ANOVA (analysis of variance) table splits the sum of squares into its components.

Total sums of squares
= Residual (or error) sum of squares + Regression (or explained) sum of squares.

Thus Σ _i (y_i - ybar)² = Σ _i (y_i - yhat_i)² + Σ _i (yhat_i - ybar)²
where yhat_i is the value of y_i  predicted from the regression line
and ybar is the sample mean of  y.

For example:
R² = 1 - Residual SS / Total SS    (general formula for R²)
     = 1 - 0.4/2.0            (from data in the ANOVA table)
     = 0.8                        (which equals R² given in the regression Statistics table).

The remainder of the ANOVA table is described in more detail in Excel: Multiple Regression.
 

INTERPRET REGRESSION COEFFICIENTS TABLE
 

	Coefficient	Standard error	t Stat	P-value	Lower 95%	Upper 95%
Intercept	0.8	0.38297	2.089	0.1279	-0.4188	2.0188
HH SIZE	0.4	0.11547	3.464	0.0405	0.0325	0.7675

The population regression model is:    y = β₁ + β₂ x + u
where the error u is assumed to be distributed independently with mean 0 and constant variance.

Here we focus on inference on β₂, using the row that begins with hh size.
Similar interpretation is given for inference on β₁, using the row that begins with intercept.

The column "Coefficient" gives the least squares estimates of β₁ and β₂.

The column "Standard error" gives the standard errors (i.e.the estimated standard deviation) of the least squares estimate of β₁ and β₂ .

The second row of the column "t Stat" gives the computed t-statistic for H0: β₂ = 0 against Ha: β₂ ≠ 0.
This is the coefficient divided by the standard error: here 0.4 / 0.11547 = 3.464.
It is compared to a T distribution with (n-k) degrees of freedom where here n = 5and k = 2.

The column "P-value" gives for hh size are for H0: β₂ = 0 against Ha: β₂ ≠ 0.
This equals the Pr{|T| > t-Stat}where T is a T-distributed random variable with n-k degreres of freedom and t-Stat is the computed value of the t-statistic given is the previous column.
Note that this P-value is for a 2-sided test.
For a 1-sided test divide this P-value by 2 (also checking the sign of the t-Stat).

The columns "Lower 95%" and "Upper 95%" values define a 95% confidence interval for β₂.

A simple summary of the above output is that

• The fitted line is y = 0.8+0.4*x
• The slope coefficient has estimated standard error of 0.115
• The slope coefficient has t-statistic of 3.464.
• The slope coefficient has p-value of 0.0405.
  
• The 95% confidence interval for β₂  is (0.0325, 0.7675).
• There are 5 observations and 2 regressors (intercept and x) so in inference we use T(5-2) =T(3).
• A measure of the fit of the model is R² = 0.8.
  
• The standard error of the regression is 0.365148.
  

95% confidence interval for slope coefficient β₂ is from Excel output (.0325, .7675).

Excel computes this as
   b₂ ± t_.025(3) × se(b₂)
= 0.8 ± TINV(0.05, 3) × 0.11547
= 0.8 ± 3.182 × 0.11547
= 0.8 ± .367546
= (.0325,.7675).

Other confidence intervals can be obtained.
For example, to find 99% confidence intervals: in the Regression dialog box (in the Data Analysis Add-in),
check the Confidence Level box and set the level to 99%.

Excel automatically gives output to make this test easy.

Consider test H0: β₂ = 0 against Ha: β₂ ≠ 0 at significance level α = .05.

Using the p-value approach

• From the output p-value = 0.0405.
  
• Reject the null hypothesis at level .05 since the p-value is < 0.05.

Using the critical value approach

• From the output t-statistic = 3.464.
• The critical value is t_.025(3) = TINV(0.05,3) = 3.182.
• So reject null hypothesis at level .05 since t = 3.464 > 3.182.

• For the p-value approach the reported p-value is for a two-sided test and needs to be halved for a one-sided test: p = 0.0405/2 = 0.202.
• For the t-statistic approach the reported t-statistic is appropriate but the critical value is now t_.05(3) = TINV(0.10,3) = 2.353.
• Further refinement is needed depending on the direction of the one-tailed test. See a textbook.  
  

TEST HYPOTHESIS OF SLOPE COEFFICIENT EQUAL TO VALUE OTHER THAN ZERO

For non-zero hypthesized value of the slope parameter we need to manually do the computations.
 
Consider test H0: β₂ = 1 against Ha: β₂ ≠ 1 at significance level α = .05.
This is that an extra household member means an extra car.

Then
  t = (b₂ - H0 value of β₂) / (standard error of b₂ )
    = (0.4 - 1.0) / 0.11457
    = -5.196.

Using the p-value approach

• p-value = TDIST(5.196, 3, 2) = 0.0138.
• Reject the null hypothesis at level .05 since the p-value is < 0.05.

• We computed  t = 5.196
• The critical value is t_.025(3) = TINV(0.05,3) = 3.182.
• So reject null hypothesis at level .05 since t = 5.196 > 3.182. 
  

FITTED VALUES AND RESIDUALS FROM REGRESSION LINE

Fitted values and residuals from the regression line.
  

y =CARS	x = HH SIZE	yhat = 0.8+0.4*x	e = y - yhat
1	1	1.2	-.2
2	2	1.6	0.4
2	3	2.0	0.0
2	4	2.4	-.4
3	5	2.8	0.2

These can be obtained using the Regression dialog box in the Data Analysis regression Add-in,
by checking the Residuals box.