MULTIPLE REGRESSION USING THE DATA ANALYSIS ADD-IN
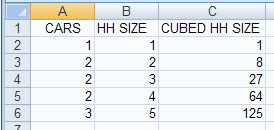
We then create a new variable in cells C2:C6, cubed household size
as
a regressor.
Then in cell C1 give the the heading CUBED HH SIZE.
(It turns out that
for the se data squared HH SIZE has a coefficient of exactly 0.0 the
cube is used).
The spreadsheet cells A1:C6 should look like:

We have regression with an intercept and the regressors HH SIZE and CUBED HH SIZE
The population regression model is: y = β1
+ β2 x2 + β3 x3 + u
It is assumed that the error u is independent with constant variance
(homoskedastic) - see EXCEL LIMITATIONS at the bottom.
We wish to estimate the regression line: y =
b1 + b2 x2 + b3 x3
We do this using the Data analysis Add-in and Regression.
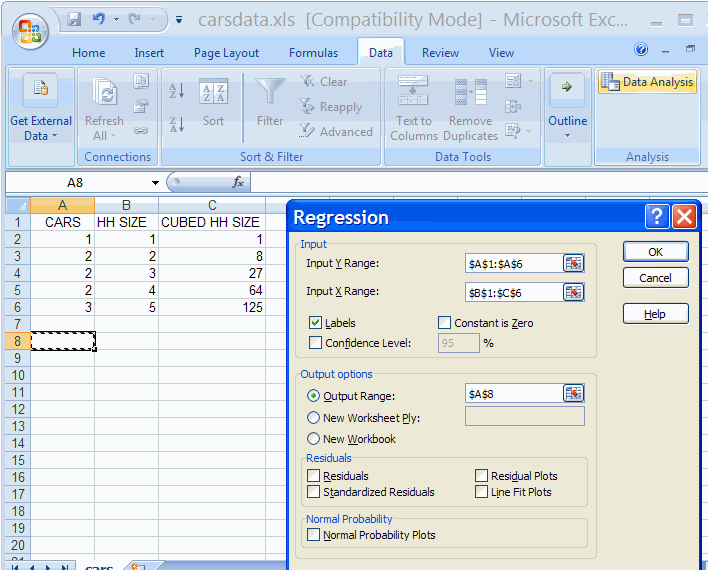
The only change over one-variable regression is to include more than
one column in the Input X Range.
Note, however, that the regressors need to be in contiguous columns
(here columns B and C).
If this is not the case in the original data, then columns need to be
copied to get the regressors in contiguous columns.
Hitting OK we obtain
The regression output has three components:
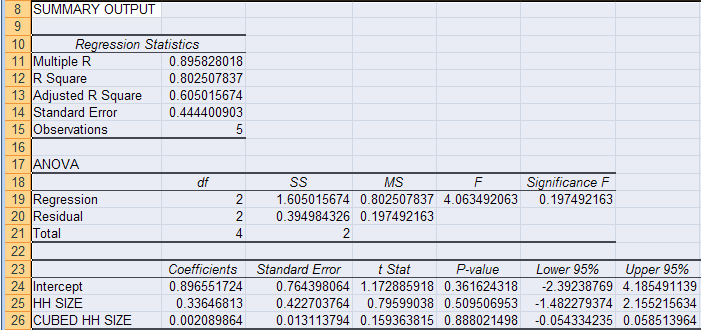
This is the following output. Of greatest interest is R Square.
| Explanation | ||
| Multiple R | 0.895828 | R = square root of R2 |
| R Square | 0.802508 | R2 |
| Adjusted R Square | 0.605016 | Adjusted R2 used if more than one x variable |
| Standard Error | 0.444401 | This is the sample estimate of the standard deviation of the error u |
| Observations | 5 | Number of observations used in the regression (n) |
The above gives the overall goodness-of-fit measures:
R2 = 0.8025
Correlation between y and y-hat is
0.8958
(when squared gives 0.8025).
Adjusted R2 = R2 -
(1-R2 )*(k-1)/(n-k)
= .8025 - .1975*2/2 = 0.6050.
The standard error here refers to the estimated standard deviation
of
the error term u.
It is sometimes called the standard error of the regression. It equals
sqrt(SSE/(n-k)).
It is not to be confused with the standard error of y itself (from
descriptive statistics) or with the standard errors of the regression
coefficients
given below.
R2 = 0.8025 means that
80.25% of the variation of yi around ybar (its mean) is
explained by the regressors x2i and x3i.
INTERPRET ANOVA TABLE
An ANOVA table is given. This is often skipped.
| df | SS | MS | F | Significance F | |
| Regression | 2 | 1.6050 | 0.8025 | 4.0635 | 0.1975 |
| Residual | 2 | 0.3950 | 0.1975 | ||
| Total | 4 | 2.0 |
The ANOVA (analysis of variance) table splits the sum of squares into its components.
Total sums of squares
= Residual (or error) sum of squares + Regression (or explained) sum
of squares.
Thus Σ
i (yi - ybar)2 = Σ
i (yi - yhati)2 + Σ
i (yhati - ybar)2
where yhati is the value of yi predicted
from the regression line
and ybar is the sample mean of y.
For example:
R2 = 1 - Residual SS / Total SS (general
formula for R2)
= 1 -
0.3950 / 1.6050
(from data in the ANOVA table)
=
0.8025
(which equals R2 given in the regression Statistics table).
The column labeled F gives the overall F-test of H0: β2 =
0 and β3 =
0 versus Ha: at least one of β2 and β3 does not
equal zero.
Aside: Excel computes F this as:
F = [Regression SS/(k-1)] / [Residual SS/(n-k)] = [1.6050/2] /
[.39498/2]
= 4.0635.
The column labeled significance F has the associated P-value.
Since
0.1975 > 0.05, we do not reject H0 at signficance level 0.05.
Note: Significance F in general = FINV(F, k-1, n-k) where k is
the number of regressors including hte intercept.
Here FINV(4.0635,2,2) = 0.1975.
INTERPRET REGRESSION COEFFICIENTS TABLE
The regression output of most interest is the following table of
coefficients
and associated output:
| Coefficient | St. error | t Stat | P-value | Lower 95% | Upper 95% | |
| Intercept | 0.89655 | 0.76440 | 1.1729 | 0.3616 | -2.3924 | 4.1855 |
| HH SIZE | 0.33647 | 0.42270 | 0.7960 | 0.5095 | -1.4823 | 2.1552 |
| CUBED HH SIZE | 0.00209 | 0.01311 | 0.1594 | 0.8880 | -0.0543 | 0.0585 |
Let βj denote the population coefficient of the jth regressor (intercept, HH SIZE and CUBED HH SIZE).
Then
y = 0.8966 + 0.3365*x + 0.0021*z
CONFIDENCE INTERVALS FOR SLOPE COEFFICIENTS
95% confidence interval for slope coefficient β2 is from Excel output (-1.4823, 2.1552).
Excel computes this as
b2 ± t_.025(3) × se(b2)
= 0.33647 ± TINV(0.05, 2) × 0.42270
= 0.33647 ± 4.303 × 0.42270
= 0.33647 ± 1.8189
= (-1.4823,
2.1552).
TEST HYPOTHESIS OF ZERO SLOPE COEFFICIENT ("TEST OF STATISTICAL SIGNIFICANCE")
The coefficient of HH SIZE has estimated standard error of 0.4227,
t-statistic
of 0.7960 and p-value of 0.5095.
It is therefore statistically insignificant at significance level α =
.05 as p > 0.05.
The coefficient of CUBED HH SIZE has estimated standard error of
0.0131,
t-statistic of 0.1594 and p-value of 0.8880.
It is therefore statistically insignificant at significance level α =
.05 as p > 0.05.
There are 5 observations and 3 regressors (intercept and x) so we
use
t(5-3)=t(2).
For example, for HH SIZE p = =TDIST(0.796,2,2) = 0.5095.
TEST HYPOTHESIS ON A REGRESSION PARAMETER
Here we test whether HH SIZE has coefficient β2 = 1.0.
Example: H0: β2 = 1.0 against
Ha: β2 ≠ 1.0 at significance
level α = .05.
Then
t = (b2 - H0 value of β2) / (standard
error of b2
)
= (0.33647 - 1.0) / 0.42270
= -1.569.
Using the p-value approach
OVERALL TEST OF SIGNIFICANCE OF THE REGRESSION PARAMETERS
We test H0: β2 = 0 and β3 =
0 versus Ha: at least one of β2 and β3 does not
equal zero.
From the ANOVA table the F-test statistic is 4.0635 with p-value of
0.1975.
Since the p-value is not less than 0.05 we do not reject the null
hypothesis
that the regression parameters are zero at significance level 0.05.
Conclude that the parameters are jointly statistically insignificant
at significance level 0.05.
Note: Significance F in general = FINV(F, k-1, n-k) where k is
the number of regressors including hte intercept.
Here FINV(4.0635,2,2) = 0.1975.
PREDICTED VALUE OF Y GIVEN REGRESSORS
Consider case where x = 4 in which case CUBED HH SIZE = x^3 = 4^3 = 64.
yhat =
b1 + b2 x2 + b3 x3
= 0.88966 + 0.3365×4 + 0.0021×64
= 2.37006
EXCEL LIMITATIONS
Excel restricts the number of regressors (only up to 16 regressors ??).
Excel requires that all the regressor variables be in adjoining
columns.
You may need to move columns to ensure this.
e.g. If the regressors are in columns B and D you need to copy at least
one of columns B and D so that they are adjacent to each other.
Excel standard errors and t-statistics and p-values are based on the
assumption that the error is independent with constant variance
(homoskedastic).
Excel does not provide alternaties, such asheteroskedastic-robust or
autocorrelation-robust standard errors and t-statistics and p-values.
More specialized software such as STATA, EVIEWS, SAS, LIMDEP, PC-TSP,
... is needed.
For further information on how to use Excel go to
http://cameron.econ.ucdavis.edu/excel/excel.html