GENERAL COMMENTS ON USE OF T-DISTRIBUTION
The most commonly used confidence intervals and hypothesis tests for the population mean use the t-distribution. These are the ones we present, and the ones that the latest versions of Excel produce in descriptive statistics.
The underlying theory to justify this assumes normally distributed data, i.e. that the individual observations are independent and identically distributed observations from a normal distribution with mean µ (mu) and unknown variance σ (sigma).
What if the data are not normal, though are still independent and identically distributed observations with mean µ and unknown variance σ^2?
Critical values and p-values for the t-distribution are obtained
using functions TDIST and TINV.
See Excel 2007: DIST, TINV,
NORMSDIST and NORMSINV
CONFIDENCE INTERVALS FOR THE POPULATION MEAN µ
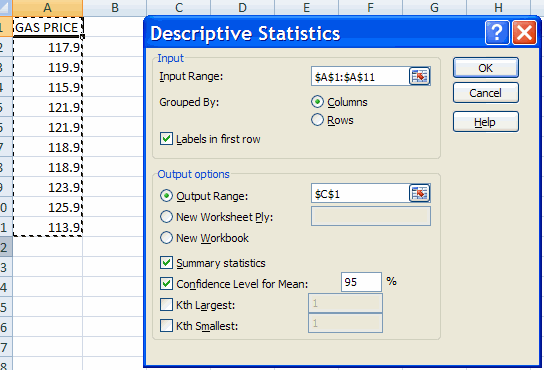
We consider gasoline price data (cents per gallon) in file gasolinepricedata.csv

This yields
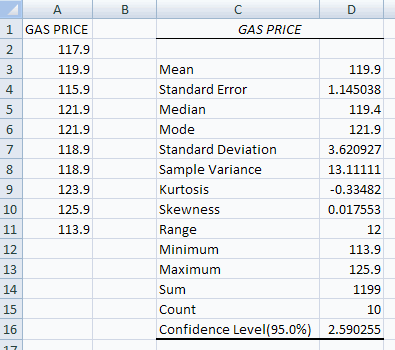
Then a 95% confidence interval for the population mean is
Interpretation: This means that with probability 0.95 the sample comes from a data generating process with population mean µ in the range 117.31 to 122.49.
To obtain confidence intervals at other levels of confidence, e.g. 90%, in Data | Analysis | Data Analysis | Descriptive Statistics change the confidence level for the mean from its default of 95% to e.g. 90%.
Note that since the sample is small here (n=10) this test requires
the
assumption that the data are normally distributed (see GENERAL COMMENTS
at the top of this handout).
This assumption is impossible to test with
only ten observations, but could be justified if (and I say if)
experience
with other larger samples of gasoline price data suggests that this is
a resonable assumption.
FURTHER DETAILS ON CONFIDENCE INTERVALS FOR THE POPULATION MEAN
µ
In general a symmetric confidence interval is of the form:
estimate of the parameter of interest
±
critical value × standard error.
For this particular problem, a 95% confidence interval for the
population
mean µ, when x is normal(µ,σ), is
sample mean ± t(.025; n-1) ×
s/sqrt(n)
which can be calculated manually in Excel using:
THE CONFIDENCE( ) FUNCTION IS NOT USED.
In Formula Tab | Function Library | More Functions | Statistical is
a function CONFIDENCE( ).
This computes the "Confidence level" when the standard deviation is
known.
This is z(.025) × σ/sqrt(n) for a 95% confidence interval.
We do not use this function because in economics examples σ is unknown
and we instead use t(.025; n-1) × s/sqrt(n)
In summary, we do not use the CONFIDENCE( ) function as it leads to
different results than Descriptive Statistics.
HYPOTHESIS TESTS FOR THE POPULATION MEAN µ
Hypothesis Tests for the Population Mean
Excel does not have an automatic command and output for hypothesis
testing
on the population mean.
Instead one needs to manually perform the hypothesis test using output
from descriptive statistics.
We distinguish between one-sided and two-sided tests.
Let µ0 denote the hypothesized value of µ.
Two-sided test: H0: µ = µ0 against
Ha: µ
not equal to µ0
One-sided test: H0: µ <= µ0
against Ha: µ > µ0
or: H0: µ >= µ0 against Ha: µ
< µ0
We first find the value of a test statistic.
We then use either the p-value approach or the critical value approach
to reject or not reject the null hypothesis that µ = µ0.
Test Statistic
A test statistic is often of the form:
(estimated value - hypothesized value) / standard
error
where the standard error gives the precision of the estimate.
For tests of H0: µ = µ0 we use the t-test statistic:
t = (Xbar - µ0) / (s/sqrt(n)).
For the example here, to test H0: µ = 118 using the above
data,
t = (119.9 - 118) / 1.145038 = 1.659.
The t-statistic is t-distributed with (n-1) degrees of freedom under the null hypothesis that µ = µ0 and assuming that the individual observations are independent and identically distributed observations from a normal distribution with mean µ.
Note that since the sample is small here (n=10) this test requires
the
assumption that the data are normally distributed (see GENERAL COMMENTS
at the top of this handout).
This assumption is impossible to test with
only ten observations, but could be justified if (and I say if)
experience
with other larger samples of gasoline price data suggests that this is
a reasonable assumption.
p-value approach
The p-value is the probability of just rejecting the null hypothesis.
In general we reject the null hypothesis at level α (alpha) if the
p-value
< α
and do not reject the null hypothesis at level α if the p-value
>= α.
[A common choice of α is 0.05].
Let T be a t-distributed random variable and t be the calculated value of the test statistic.
The p-value for hypothesis tests on the population mean µ is then obtained using the Excel commands:
More generally we will have a different test statistic value than 1.659 and a different number of degrees of freedom than 9.
Critical values
Critical values are used to define a critical region.
If the calculated value of the test statistic falls in critical region then the null hypothesis is rejected. Otherwise it is not rejected.
Let c be the critical value of the test statistic and consider tests at level α (often α = .05).
The critical for hypothesis tests on the population mean µ is then obtained using the Excel commands:
Note that since the sample is small here (n=10) this test requires
the
assumption that the data are normally distributed (see GENERAL COMMENTS
at the top of this handout).
This assumption is impossible to test with
only ten observations, but could be justified if (and I say if)
experience
with other larger samples of gasoline price data suggests that this is
a resonable assumption.
THE ZTEST( ) AND TTEST( ) FUNCTIONS ARE NOT USED.
In Formula Tab | Function Library | More Functions | Statistical is
a function ZTEST( ).
This computes the t-test when the standard deviation is known.
It computes p-values using standard normal rather than t-distribution.
We do not use this function because in economics examples σ is unknown
and we instead use the t-distribution.
In Formula Tab | Function Library | More Functions | Statistical is
a function TTEST( ).
This performs a t-test of the difference im neans in two different
samples.
This is a different t-test to the one presented above, where just a
single sample is used.
The TEST( ) function does not do the t-test given above.
For further information on how to use Excel go to
http://cameron.econ.ucdavis.edu/excel/excel.html